论文概览
论文标题:Enhancing Reasoning through Process Supervision with Monte Carlo Tree Search
研究机构:AI Lab
基座模型:Llama-3.1-8B-Instruct, DeepSeek-Math-7B-Instruct
论文地址:https://arxiv.org/abs/2501.01478
核心创新:将蒙特卡洛树搜索与自训练相结合,通过过程监督提升推理能力
主要成果:在MATH数据集上提升4.85%,GSM8K上提升5.03%
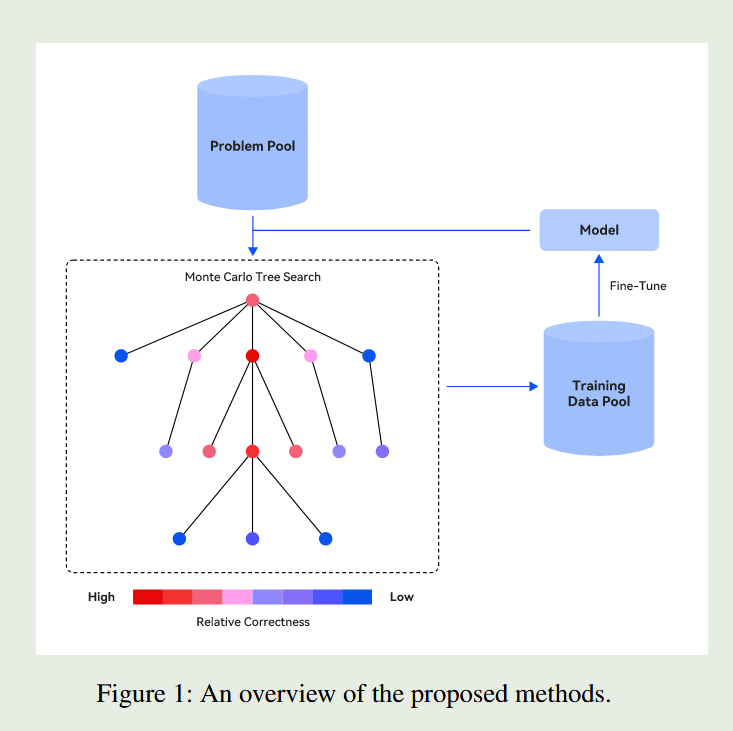
核心贡献
本文提出了一个创新的自训练框架,巧妙地将蒙特卡洛树搜索与过程监督结合:
- MCTS引导的数据生成:利用蒙特卡洛树搜索系统性地探索推理路径,生成高质量训练数据
- 过程级监督信号:不仅关注最终答案,更重视每个推理步骤的质量评估
- 迭代自我提升:通过多轮生成-训练循环,模型能力逐步提升
- 跨任务泛化:训练得到的推理能力能够有效迁移到不同任务
问题背景:推理训练的挑战
传统自训练的困境
虽然自训练(Self-Training)是提升模型能力的有效方法,但在推理任务中面临独特挑战:
1. 探索效率低下
- 随机采样很难找到高质量的推理路径
- 大部分生成的推理过程都是错误的
- 缺乏系统性的探索策略
2. 监督信号稀疏
- 只有最终答案的对错反馈信息量有限
- 无法区分"歪打正着"和"正确推理"
- 难以识别推理过程中的关键错误步骤
3. 数据质量参差不齐
- 错误的推理步骤会误导模型学习
- 缺乏有效的质量筛选机制
- 可能加强模型的错误推理模式
核心洞察:树搜索遇上过程监督
问题的关键在于:如何系统性地探索推理空间,并对每个推理步骤给出准确的质量评估?
本文的创新思路是将问题建模为树搜索过程:
- 每个推理步骤对应树中的一个节点
- MCTS算法系统性地探索最有希望的推理路径
- 过程监督为每个步骤提供细粒度的质量评估
技术方法详解
数据生成:MCTS驱动的推理探索
问题建模:推理即树搜索
我们将推理过程建模为一棵树:
- 根节点:问题本身
- 中间节点:部分推理过程
- 叶子节点:完整的解答
- 边:从一个推理状态到下一个状态的转换
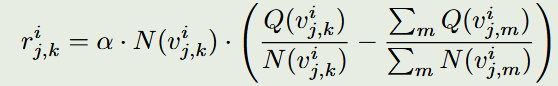
MCTS四步曲:系统性探索推理空间
1. 选择(Selection) 从根节点开始,使用UCB(Upper Confidence Bound)策略选择最有希望的子节点:
- 平衡探索(exploration)和利用(exploitation)
- 优先选择既有潜力又未充分探索的路径
- 一直向下搜索直到找到未完全扩展的节点
2. 扩展(Expansion) 在选中的节点处生成新的推理步骤:
- 使用LLM以非零温度采样下一步推理
- 每次扩展增加一个新的子节点
- 确保探索的多样性
3. 模拟(Simulation) 从新扩展的节点继续推理直到得到最终答案:
- 使用LLM完成剩余的推理过程
- 评估最终答案的正确性
- 获得本次探索的奖励信号
4. 回传(Backpropagation) 将奖励信号向上传播,更新路径上所有节点的统计信息:
- 正确答案:奖励 = 1.0
- 错误答案:奖励 = 0.0
- 更新访问次数和累积奖励
过程级质量评估
对于每个推理步骤,我们计算其质量分数:
$$r_{j,k}^i = \alpha \times \frac{Q(v_{j,k}^i)}{N(v_{j,k}^i)}$$
其中:
- $Q(v_{j,k}^i)$:节点的累积奖励
- $N(v_{j,k}^i)$:节点的访问次数
- $\alpha$:缩放常数
这个分数反映了该推理步骤的**“相对正确度”**,即在多次探索中,通过这个步骤最终得到正确答案的概率。
训练数据构建
经过MCTS搜索后,我们得到高质量的训练数据:
$$D = {(x_i, p_j^i, s_j^i, c_j^i)}$$
其中:
- $x_i$:第$i$个问题
- $p_j^i$:问题$x_i$的第$j$个部分解
- $s_j^i$:部分解$p_j^i$的下一步推理
- $c_j^i$:分配给$s_j^i$的质量分数
数据筛选策略:
- 只保留质量分数大于0的推理步骤
- 避免错误推理步骤污染训练数据
- 确保训练数据的高质量
迭代训练:螺旋上升的能力提升
损失函数设计
我们使用加权损失函数进行训练:
$$\mathcal{L}(\theta_i) = -\sum_{(x,p,s,c) \in D} c \cdot \log \pi_{\theta_i}(s|x,p) + \beta \cdot D_{KL}(\pi_{\theta_i}(\cdot|x,p) || \pi_{\theta_{i-1}}(\cdot|x,p))$$
第一项:加权负对数似然
- 高质量的推理步骤获得更大的训练权重
- 让模型更多地学习正确的推理模式
第二项:KL散度正则化
- 防止模型在训练过程中发生剧烈的分布漂移
- 保持与上一轮模型的合理距离
- 借鉴了RLHF中的稳定性技巧
迭代流程
- 第0轮:从预训练模型开始
- 第i轮:
- 使用第$(i-1)$轮的模型进行MCTS数据生成
- 训练得到第$i$轮模型
- 评估性能提升
- 重复:直到性能收敛
这种迭代方式让模型能够:
- 自我纠错:发现并修正之前的推理错误
- 能力扩展:探索更复杂的推理路径
- 知识巩固:强化正确的推理模式
实验结果:数据说话
主要性能提升
在两个主要数学推理基准上的结果:
MATH数据集(Llama-3.1-8B-Instruct):
- 基础模型:47.07%
- 第1轮训练:50.04% (+2.97%)
- 第4轮训练:51.92% (+4.85%)
GSM8K数据集(DeepSeek-Math-7B-Instruct):
- 基础模型:80.77%
- 第1轮训练:85.35% (+4.58%)
- 第2轮训练:85.80% (+5.03%)
与基线方法对比
| 方法 | MATH | GSM8K |
|---|---|---|
| Zero-shot-CoT | 47.07 ± 0.15 | 80.77 ± 0.25 |
| RFT | 47.96 ± 0.21 | 83.33 ± 0.25 |
| Step-level DPO | 48.48 ± 0.27 | 82.55 ± 0.17 |
| 我们的方法 | 51.92 ± 0.20 | 85.80 ± 0.22 |
关键洞察:
- 相比传统的拒绝采样微调(RFT),我们的方法提升更显著
- 相比Step-level DPO,MCTS的系统性探索带来更大收益
- 迭代训练确实能够持续提升模型能力
跨任务泛化能力
我们还验证了方法的泛化能力:
GSM8K → MATH:
- 在GSM8K上训练的模型在MATH上仍有提升
- 第2轮:48.74% (vs 基础47.07%)
MATH → GSM8K:
- 在MATH上训练的模型在GSM8K上表现稳定
- 第2轮:85.72% (vs 基础80.77%)
这说明我们的方法学到的是通用的推理能力,而非任务特化的技巧。
技术创新点
1. MCTS与自训练的有机结合
- 首次将蒙特卡洛树搜索应用于大语言模型的自训练
- 系统性地探索推理空间,避免随机采样的低效性
2. 过程级监督信号
- 不仅关注最终答案,更重视推理过程的质量
- 为每个推理步骤提供细粒度的质量评估
3. 迭代能力提升机制
- 通过多轮生成-训练循环实现螺旋上升
- KL正则化确保训练过程的稳定性
4. 通用性强
- 适用于不同的基础模型和推理任务
- 具有良好的跨任务泛化能力
局限性与未来方向
当前挑战
- 计算成本较高:MCTS搜索需要大量的前向推理计算
- 超参数敏感:UCB参数、温度设置等需要仔细调优
- 评估方式限制:目前主要依赖最终答案的正确性评估
未来展望
- 搜索效率优化:开发更高效的搜索策略和剪枝技术
- 更丰富的奖励信号:结合过程奖励模型提供更细粒度的反馈
- 扩展到更多任务:将方法推广到代码生成、科学推理等领域
论文翻译:https://dppemvhuzp.feishu.cn/docx/W84qdm5AAoienmxFl17cU7OOnkg?from=from_copylink