论文概览

论文标题：ReasonFlux: Hierarchical LLM Reasoning via Scaling Thought Templates

研究机构：Princeton University, Peking University

代码仓库：https://github.com/Gen-Verse/ReasonFlux

基座模型：Qwen2.5-32B-Instruct

论文地址：https://arxiv.org/pdf/2502.06772

计算资源：8 × NVIDIA A100 GPU

重要说明：这是SUPERCORRECT同一作者团队的续作，在师生协作基础上进一步发展的分层推理框架。

ReasonFlux框架图

核心创新

ReasonFlux 是SUPERCORRECT的自然延续，提出了一个全新的分层推理范式：

  1. 结构化思维模板库：构建包含500个精选思维模板的高效检索系统
  2. 分层强化学习：在思维模板轨迹上进行优化，而非传统的CoT轨迹
  3. 自适应推理扩展：动态选择最合适的模板组合来解决复杂问题
  4. 超越SOTA性能：在数学推理任务上超越了OpenAI o1-preview和DeepSeek-V3

ReasonFlux结果对比

问题背景：推理扩展的挑战

当前推理方法的困境

虽然O1、Gemini-2.0、DeepSeek-V3等模型在推理任务中表现不俗，但面对真正复杂的问题时，仍然力不从心：

  1. 搜索空间过大：像AIME这样的数学竞赛题需要在庞大的解空间中进行精细搜索
  2. 计算成本高昂：现有的MCTS、ToT等方法虽然有效，但计算开销巨大
  3. 探索-利用失衡：很难在"广泛探索"和"深度利用"之间找到最佳平衡点

现有方案的局限性

刻意搜索方法（如ToT、GoT）：

  • ✅ 能够探索多种推理路径
  • ❌ 计算成本随搜索空间指数增长
  • ❌ 依赖手动设计的搜索策略

奖励模型引导方法（如MCTS + PRM）：

  • ✅ 能够评估推理步骤质量
  • ❌ 采样的随机性阻碍了高效识别最优路径
  • ❌ 在复杂任务中泛化能力有限

核心洞察：模板化的分层推理

问题的关键在于：如何让模型像经验丰富的数学家一样，先选择合适的解题策略，再执行具体步骤？

ReasonFlux的核心思想是将推理过程分为两个层次：

  • 高层规划：选择合适的思维模板序列
  • 低层执行：将模板实例化为具体的推理步骤

技术方法详解

第一步：构建结构化思维模板库

为什么需要结构化？

传统的RAG方法虽然能检索相关信息，但在复杂推理中面临可扩展性问题。就像图书馆需要分类目录一样，我们需要一个结构化的模板组织方式。

模板库的精心设计

我们的每个思维模板 $T_i$ 都包含以下结构化信息：

  • $T_{nam}$：模板名称（如"$\sqrt{R^2 - x^2}$型三角代换"）
  • $T_{tag}$：关键词标签集合（如{“三角代换”, “无理函数优化”}）
  • $T_{des}$：基本原理和适用场景描述
  • $T_{sco}$：适用范围定义
  • $T_a$：详细应用步骤 ${a_1, a_2, …, a_k}$
  • $T_{exa}$：应用示例集合

整个模板库定义为： $$D_{temp} = {T_1, T_2, …, T_m}$$

其中 $m$ 是模板总数（约500个）。

模板示例

这种结构化设计的优势：

  • 高效检索：基于关键词和元数据快速定位相关模板
  • 精准匹配：根据问题特征选择最合适的解题策略
  • 可扩展性：新模板可以轻松加入而不影响整体性能

第二步：分层强化学习训练

结构感知的预训练

首先，我们让模型熟悉模板库的结构：

$$\mathcal{L}{struct} = -\mathbb{E}{(T_{nam}, T_{tag}, T_{des}, T_{sco}) \sim D_{train}} \log \pi_\theta(T_{des}, T_{sco} | T_{nam}, T_{tag})$$

这个过程让模型学会将模板的标识信息（名称和标签）与其功能特性（描述和范围）关联起来。

思维模板轨迹优化

接下来是关键创新：我们不再优化传统的CoT轨迹，而是优化思维模板轨迹 $T_{traj}$。

轨迹定义： $$T_{traj} = {s_1, s_2, …, s_n}$$

其中每个 $s_i$ 代表一个高级推理步骤，关联着特定的模板名称。

奖励机制： 我们用模板轨迹在相似问题集合上的平均表现来评估其质量：

$$R(T_{traj}) = \frac{1}{|X_{sim}|} \sum_{x_i \in X_{sim}} \text{Acc}(\pi_{inf}(x_i, T_{traj}))$$

优化目标： $$\mathcal{L}{TTR}(\theta) = -\mathbb{E}{(x, (T^+{traj}, T^-{traj})) \sim D_{pair}} \left[ \log \sigma \left( \beta \log \frac{\pi_{\theta}(T^+{traj}|x)}{\pi{sft}(T^+{traj}|x)} - \beta \log \frac{\pi{\theta}(T^-{traj}|x)}{\pi{sft}(T^-_{traj}|x)} \right) \right]$$

这里的核心思想是：让模型学会为每个问题规划最优的模板使用序列，而不是盲目地生成推理步骤。

第三步：自适应推理扩展系统

动态模板规划

推理扩展系统

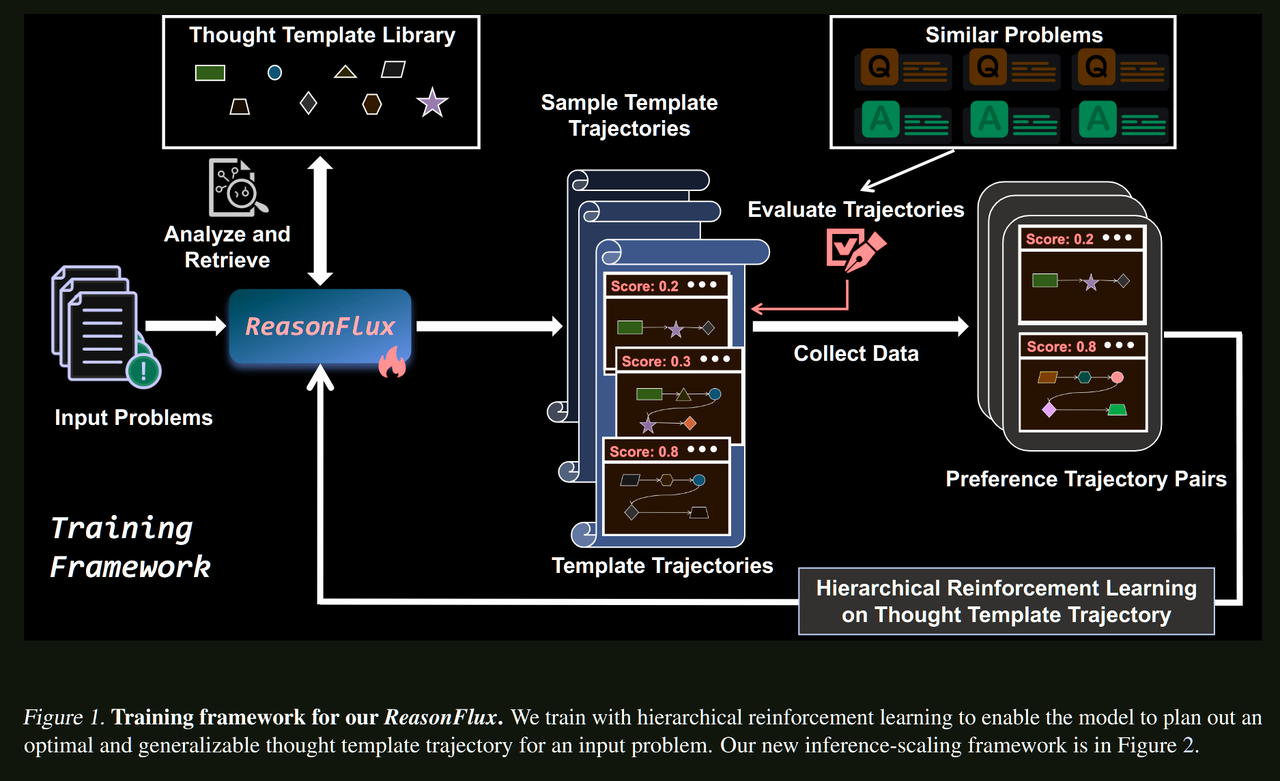
ReasonFlux的推理过程是一个优雅的分层协作：

  1. 问题分析：ReasonFlux首先抽象出问题的核心数学概念 $a(x)$

  2. 轨迹规划：基于抽象表示生成最优模板轨迹 $T^*_{traj}$

  3. 模板检索：从库中检索相关模板： $$T_{rag} = \text{ReasonFlux}({T^i_{nam}, T^i_{tag}}^n_{i=1}, D_{temp})$$

  4. 步骤实例化：将抽象步骤转化为具体推理： $$\hat{s}i = \pi{inf}(x_i, s_i, T_i)$$

迭代优化机制

更精彩的是，ReasonFlux具备自我调整能力：

  1. 评估反馈：$\delta_i = \text{ReasonFlux}(T^*_{traj}, \hat{s}_i)$
  2. 轨迹调整：$T^_{traj} \leftarrow \text{ReasonFlux}(T^_{traj}, \delta_i)$

这种机制让ReasonFlux能够：

  • 根据中间结果调整后续策略
  • 发现更高效的解决路径
  • 处理问题中隐藏的约束和机会

实验结果：全面超越SOTA

主要基准测试表现

ReasonFlux在多个数学推理基准上都取得了令人瞩目的成绩：

主要结果

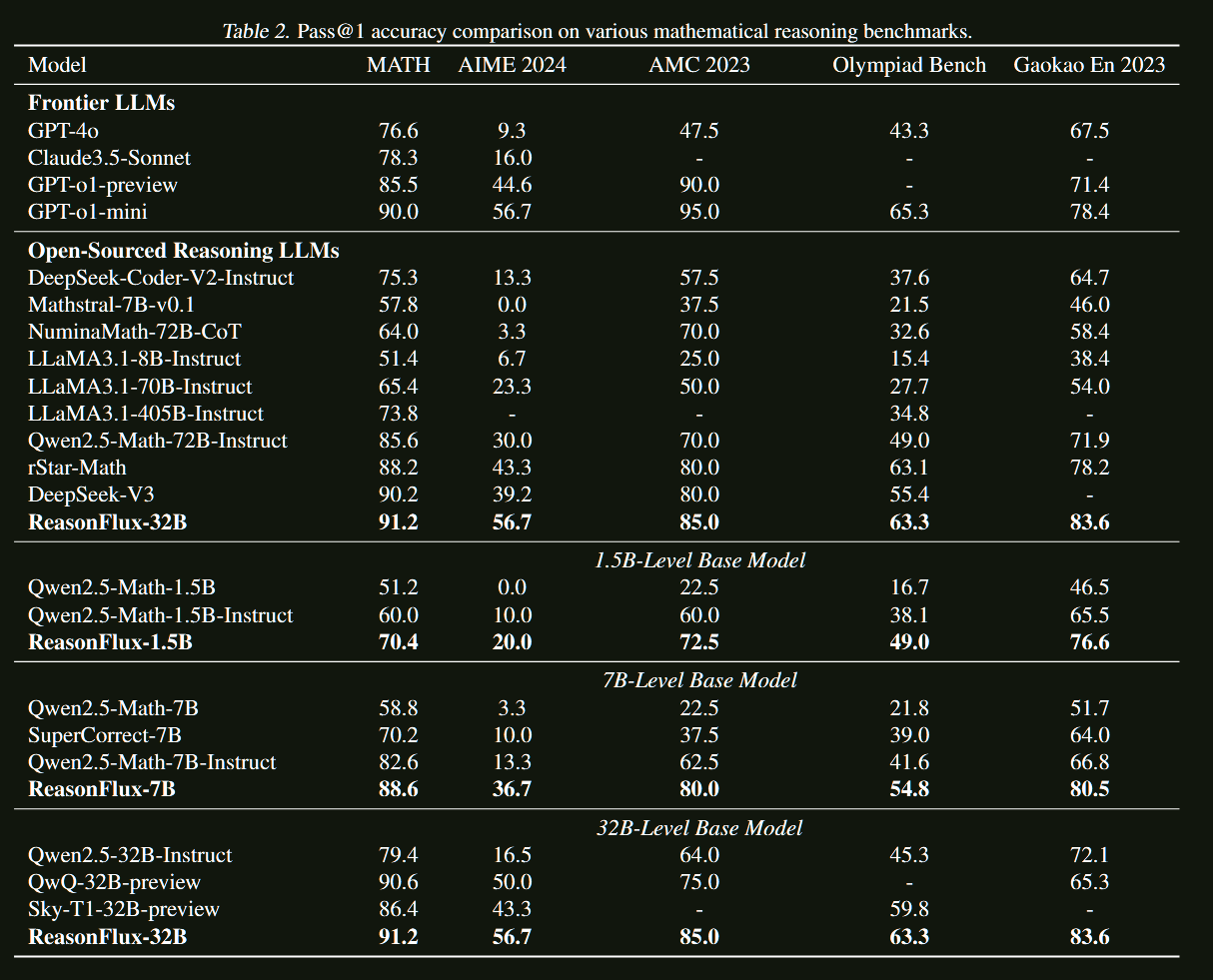
在MATH基准上：

  • 超越OpenAI o1-preview
  • 相比基线模型提升显著

在AIME基准上：

  • 达到接近人类专家的水平
  • 在最具挑战性的数学竞赛题目上表现出色

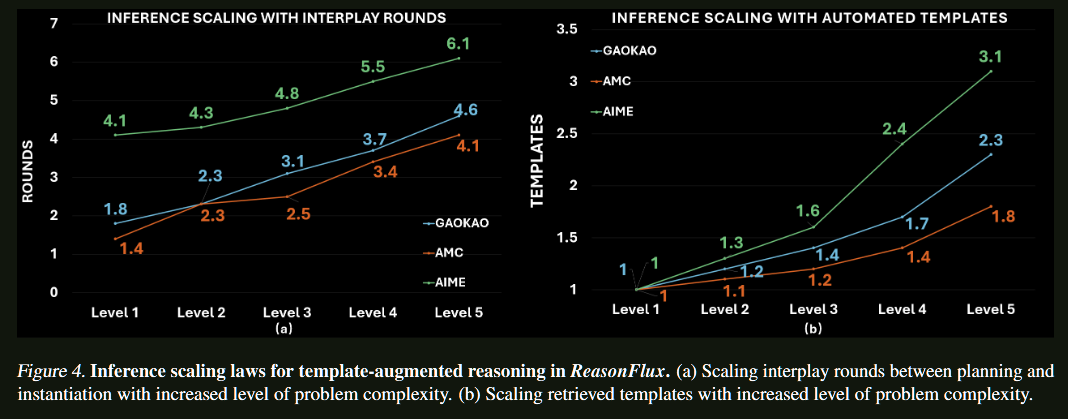
扩展性分析

扩展规律

ReasonFlux展现出优秀的扩展特性：

  • 计算效率：相比MCTS等方法，在相同计算预算下性能更优
  • 稳定提升：随着模板数量增加，性能稳步提升
  • 探索-利用平衡：在广度探索和深度利用之间找到最佳平衡点

消融研究

消融实验

各个组件的贡献分析：

  1. 结构化模板库：提供了高质量的推理指导
  2. 分层强化学习：显著提升了模板选择的准确性
  3. 自适应扩展系统：进一步优化了推理效率

案例分析

案例分析

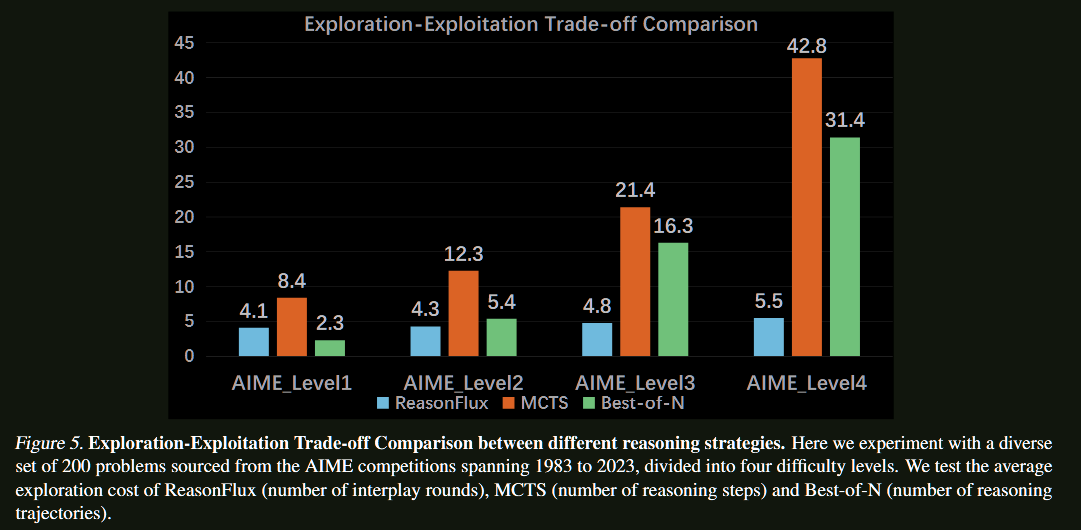
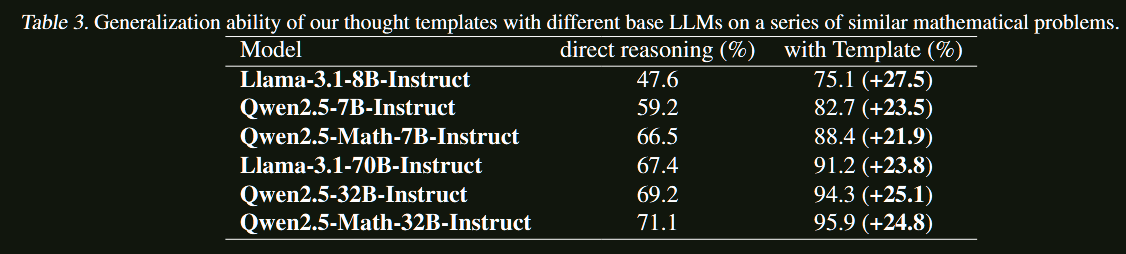
通过具体例子可以看出，ReasonFlux能够：

  • 准确识别问题类型
  • 选择合适的解题策略组合
  • 在执行过程中动态调整方案

局限性与未来方向

当前挑战

  1. 模板库维护：需要持续更新和扩展模板库以覆盖更多问题类型
  2. 领域特化：当前主要针对数学推理，其他领域的适用性有待验证
  3. 计算资源：虽然比MCTS高效，但仍需要相当的计算资源

未来展望

  1. 跨领域扩展：将分层推理框架推广到科学推理、代码生成等领域
  2. 模板自动发现：开发能够自动发现和提取新推理模板的方法
  3. 更高效的架构：探索更轻量级的实现方式，降低计算成本